On Purpose: An enquiry into the possible roles of the computer in art

This is not another article about ‘computer art’

By HAROLD COHEN

(This article was first published in Studio International, Vol 187, No 962, January 1974, pages 11-16.)

The development of the computer has brought with it a cultural revolution of massive proportions, a revolution no less massive for being almost silent. We are living now in its early stages, and it would be difficult to predict — certainly well outside the scope of this article — what changes will be effected within the next two or three decades. I think it is clear, however, that well within that period, subject to such issues as public education, the computer will have come to be regarded as a fundamental tool by almost every conceivable profession.¹ The artists may be among them. That will be the case, obviously, only if it shows itself to have something of a non-trivial nature to offer to the artist; if it can forward his purposes in some significant way.

There is little in ‘computer art’ to justify such an assumption. On the other hand I have come to believe, through my own work with the machine, that there may be more fundamental notions of purpose, and a more fundamental view of what the machine can accomplish, than we have seen so far; and this article is intended as a speculative enquiry into that proposition.

Speculation is cheap, of course, as the popular media have shown. If you fantasize any given set of capabilities for the computer, without regard to whether the real machine actually possesses them, then you can have it achieving world domination or painting pictures, falling in love or becoming paranoid; anything you wish. I would hope to offer something a little more rigorous, if rather less romantic. Thus I propose to proceed by describing the machine’s basic structure and functions, and by giving a simple account of programmes of instructions which it can handle with those functions. It should not prove necessary to make any speculation which cannot be stated in terms of these.

All the same, the undertaking is not without its difficulties. There is no doubt that the machine can forward artists’ purposes. It has forwarded a reasonable range of specific purposes already — some have been trivial, some have not — and there is no reason why that range should not be extended. But the significance of the question would seem to point to the notion of Purpose rather than purposes, implying, if not a heirarchical structure with Ultimate Purpose sitting on top as its informing principle, certainly a structure of some sort which relates all of an artist’s individual purposes.

The chain of interrogation: Why did you paint this picture blue? Why did you paint this picture? Why do you paint? is thus a good deal less innocent than it might seem at first glance. I suspect that the notion of Ultimate Purpose enjoys little currency today: but then it must follow that Purpose is not to be arrived at by backtracking up a hierarchical structure from the things that an artist does, much less from the objects he makes. The problem is rather to propose a structure which can be seen, as a whole, to account for the things the artist does. The notion of Purpose might then reasonably be thought to characterize that structure, as a whole.

Figure 1. The Hewlett Packard 2100 A computer is a small, fast, general purpose machine characteristic of the ‘minis’ now on the market.

In what terms, then, would it be possible to maintain that the use of the computer might ‘advance the artist’s Purpose’? Any claim based upon the evidence that ‘art’ has been produced would need to be examined with some care, and in the absence of any firm agreement as to what is acceptable as art we would probably want to see, at least, that the ‘art’ had some very fundamental characteristics in common with what we ordinarily view as art. This could not be done only on the basis of its physical characteristics: merely looking like an existing art object would not do. We would rather want to see it demonstrated that the machine behaviour which resulted in the ‘art’ had fundamental characteristics in common with what we know of art-making behaviour.

This is already coming close to a more speculative position: that the use of the machine might be considered to advance the artist’s Purpose if, following the earlier argument, it could be seen that this use might itself generate, or at least update, an appropriate notion of structure.

In either of these cases, it must be clear that my definitions have much in common with the curious way in which we ordinarily make our definitions of art. We would probably agree, simply on the evidence that we see around us today, that the artist considers one of his functions to be the redefinition of the notion of art.² Or we might say that the artist uses art in some way to redefine, i.e. modify himself. But since he is the agency which is responsible for the art process which effects the modification, we could restate this: the artist who uses art to modify the artist who uses art to modify…

These are recursive³ structures. I think it will become evident in due course that my definition of Purpose is recursive also; and the balance of this article may suggest that it has, in fact, been generated by my use of the machine. For the moment, though, I propose to adopt the earlier position, and to argue that the machine’s behaviour shares some very fundamental characteristics with what we normally regard as art-making behaviour. Let us now look at the computer itself, and then examine what some of these characteristics may be.

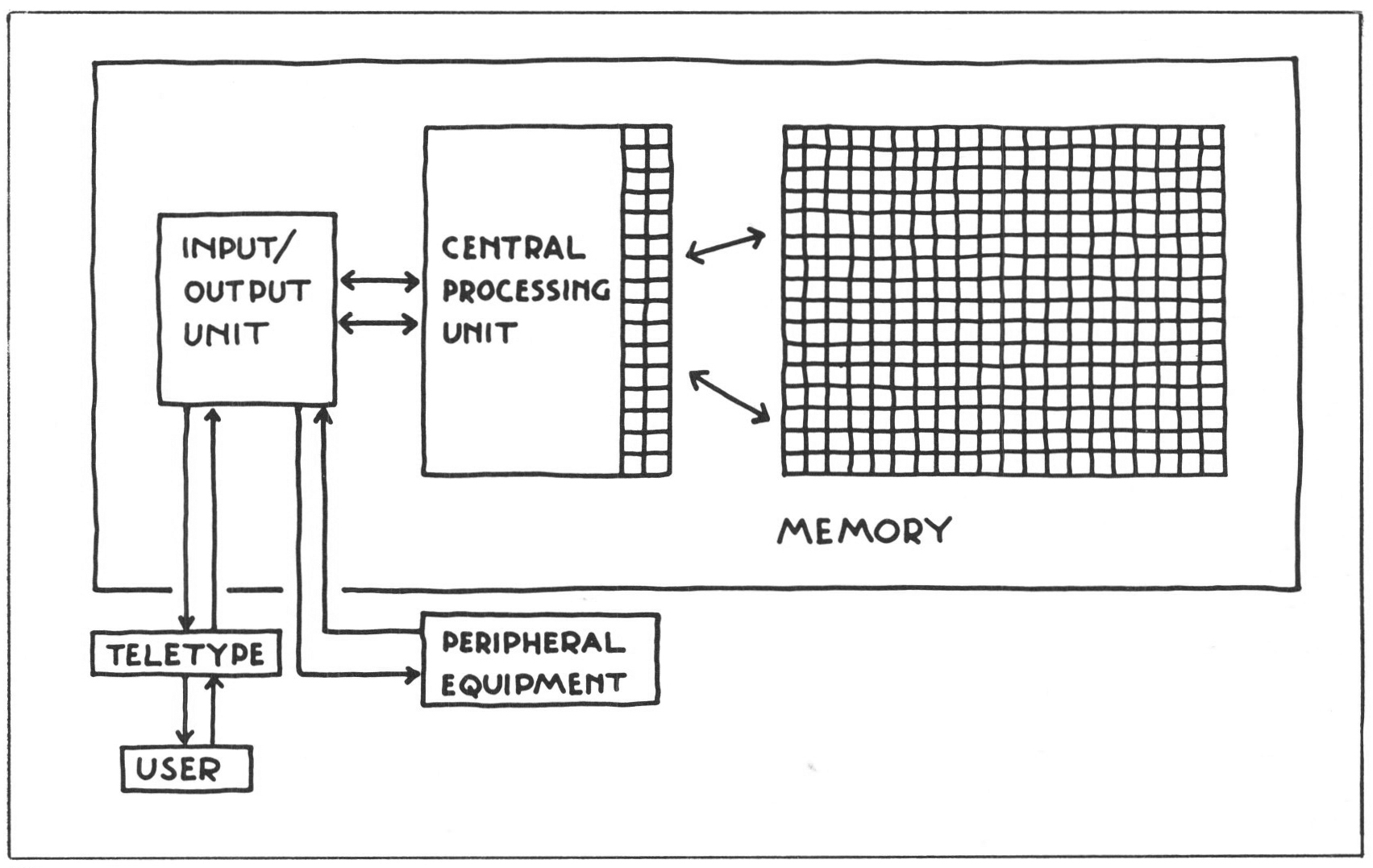
Figure 2.

There is an increasing diversity in computer design today. At one end of the spectrum machines are getting smaller, at the other end they are getting much, much bigger; at both ends they are becoming much faster. Yet it remains reasonable to talk about ‘the machine’ because, big or small, fast or slow, all computers do much the same things, and consist, diagrammatically at least, of the same parts. Part of it, usually called the Input/Output Unit, takes care of its communication with the world outside itself. Part, as you probably know, is used for storage – it is the computer’s ‘memory’. The ‘operations room’ of the whole machine, appropriately enough called the Central Processing Unit (CPU), is concerned with the processing of the stuff the machine handles, and for shifting this stuff around inside the machine. If you think of ‘memory’ as a very long string of numbered boxes, or cells, then the CPU looks after the business of storing things in the cells, labelling the cells, keeping up an index of where all the labels in use are to be found, retrieving the contents of cells with particular labels, and so on.

What are these ‘things’, this ‘stuff’ the machine handles? There are different ways of answering this question, and their relationship demonstrates one of the most significant features of the computer. Physically speaking, what the machine handles is pulses of electrical current, which are triggered by switches, and in turn trigger other switches. But the configurations into which the switches are set actually represent numbers, and the numbers represent . . . well, just about anything that can be represented numerically: quantities, dimensions and values obviously, but also anything which can be given a numerical code, like alphabetic characters, colours or instructions. The computer is a general-purpose symbol-manipulating machine, and it is capable of dealing with any problem which can be given a symbolic representation. If its accelerating use in our society rests upon its remarkable versatility, then its versatility rests in part upon the fact that a very large number of problems — much larger than you might suspect — do indeed lend themselves to symbolic, even numerical, representation.

The on-off switch might not seem too promising as a device for counting, since it can only record ‘zero’ — off, or ‘one’ — on. But a race of creatures with two-hundred and seventy-nine fingers might consider our own ten-position-switch system pretty limiting also. We still need to add a second switch to get up to 99, a third to get up to 999, and so on. Whatever ‘base’ you use for counting, how high you can count depends upon how many switches — each with the ‘base’ number of positions ù you put together. When the ‘base’ is two, you will need a large number of switches to get very far, but each of them need only have two positions — on or off: obviously an ideal situation for counting electrically. (Fig. 3.)

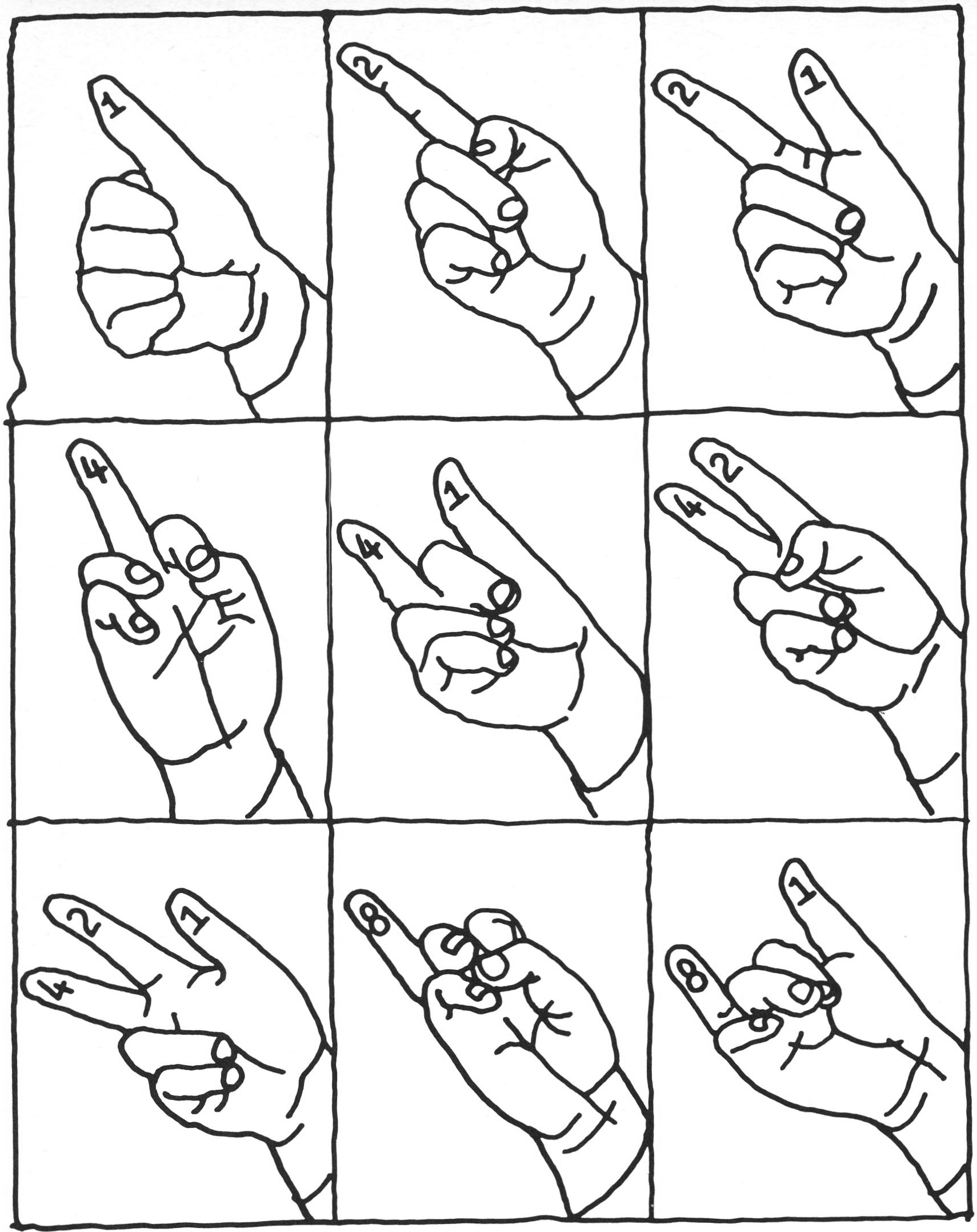
Figure 3. ‘Binary’ counting is illustrated here by hand, using each successive finger in its ‘on’ or ‘off’ positions to count successive powers of two. The total is given in each case by adding the ‘on’ fingers together.

If you were to take a somewhat less metaphorical look at those little cells in the computer’s memory, you would see that each one was in fact a string of switches. Most small modern computers have adopted sixteen as a standard, though not all: and you can figure out that this sixteen-switch cell — or ‘sixteen-bit word’, to use the jargon — will be able to hold any number up to 216-I. In a very rough sense, the size of the machine is measured by how many of these words it has in its memory, and its speed by how long it takes to retrieve one. There would probably be between four and thirty-two thousand sixteen-bit words in a small machine: up to a quarter of a million sixty-four-bit words in a big one. (Fig. 4.)

Figure 4. This memory module taken from the Hewlett Packard 2100 A computer illustrates the development of miniaturization in recent technology. The module holds 8000 sixteen-bit words — 128,000 switches in all. The switches are minute doughnut-shaped ferrite ‘cores’ strung on wires. Courtesy Hewlett Packard.

The Central Processing Unit is responsible for moving these words around, and for performing certain operations upon them. Ingeniously, it knows from the words themselves what it is to do, since several bits of each word are actually reserved for instruction codes. Thus part ‘A’ of a word might tell the CPU, ‘put the number shown in part “B” into memory’; or, ‘get the number which is in the cell in memory specified by the number in part “B” ’ ; or, ‘add the number in part “B” to the number you are now holding, and put the result back in memory’. A machine might recognize and act upon as many as fifty or sixty such instructions, but in fact most of them will be concatenations of simpler instructions, like ‘add’, ‘subtract’, ‘multiply’, ‘divide’, ‘compare’, ‘move this into memory’, ‘move this out of memory’.

The user sees nothing of all this going on. Sitting in the outside world, the set of instructions he composes for the machine will almost certainly be written in a ‘higher level’ language, like Fortran or Algol, and before the machine can execute that programme of instruction it must first run a programme of its own to translate it into its own numerical code. A single line of code — a ‘statement’ — in any higher-level language will normally break down into a large number of machine instructions, and these are executed electronically, literally by switching electrical currents, with consequent speeds measured in millionths of a second per instruction. Yet the computer’s phenomenal speed is probably less significant in accounting for its versatility than the fact that it can break down any user’s programme into the same instruction set. While the machine is running a user’s programme it can’t do anything else, so that you might say the machine is identified by the programme. But it can take on a new identity in the time it takes to clear one programme from memory and load a new one, and in a single day a moderately sized computer installation may run a thousand different programmes. A thousand different tasks, a thousand ‘different’ machines.

The man-machine relationship I am describing here is a very curious one, and not quite like any other I can think of. Nor is it possible to deal meaningfully with questions relating to what the machine can do except in terms of that relationship. It is true that the machine can do nothing not determined by the user’s programme; that the programme literally gives the machine its identity. But it is true also that once it has been given that identity, it functions as independently and as autonomously as if it had been built to perform that task and no other. Whatever is being done, it is being done by the machine.

When we talk of the computer doing something, it is implied that it is doing it, or controlling the doing of it, in the outside world. For the computer this outside world consists of any or all of a large number of special purpose devices to which it may be connected through its Input/Output Unit, varying widely in their functions from typing or punching cards, to monitoring heart beats or controlling flow-valves. Some of these ‘peripheral’ devices serve the computer in the very direct sense that they provide communication channels to the user, allowing him both to get his programme into the machine and receive its response to it. The ubiquitous teletype, and its many more sophisticated modern equivalents, serve both needs: combinations of punched-card reader and line-printer, or paper-tape reader and punch, do the same. Several peripherals function as extra memory for the machine, but then memory simply means storage, and a deck of punched cards, or a punched paper tape, is as much a storage medium as is magnetic tape or the more recently developed magnetic disc. Once a programme has been entered via the teletype or the card reader, the computer can permanently record it in any of these media, and reload it from them when required to do so. Obviously, these media can be used also for storing large quantities of information.

Above and below, figure 5a & b.

In general, you might say that the computer may receive messages from any device which is capable of putting an electrical voltage on a line, and may control any device which can be switched by a change in voltage generated by the computer. The user today has a host of peripherals at his disposal, covering a wide range of sophisticated abilities: perhaps for that very reason it is important to recognize that the use of more sophisticated peripherals does not necessarily imply more sophisticated use of the computer. If you wanted to make an animated sequence, say of a cube revolving in space, then a television-like device which could display individual frames at the rate of thirty per second would have much to commend it over a mechanical device like a plotter, whose pen only moves at five or six inches per second as it draws the frames one by one. As far as the computer is concerned, however, the task is to generate a series of views of a cube rotating in space, and it will use literally the same programme to do so regardless of what device it is addressing.

The point would seem obvious enough not to need underlining, were it not that many writers appear to hold the view that the failure of ‘computer-art’ to achieve images of notable stature can be ascribed to the lack of peripherals appropriate to the artist’s needs! Incongruously, the kind of peripheral upon the basis of which some of these writers project rosy futures for ‘computer-art’ don’t relate to new needs, but to old ones. All will be well when the artist can communicate to the computer with a paint-brush.⁴

Failure to produce significant images arises from lack of understanding, not from lack of machines. The truth is that it has been, and remains, extremely difficult for any artist to find out what he would need to know, either to use the computer, or even to overcome his certainty that he couldn’t possibly do it for himself. He will almost inevitably find himself confronted by professionals who are more than anxious to help him, but that might be a large part of his problem. ‘What will the machine do?’ he asks. ‘Well’, he is told, ‘it will do A, B, C, or D. You just choose which you want and we will programme it for you I’ The specialist is well-intentioned, and it seems unreasonable to blame him if he is less than well-informed about what the artist wants. Surprisingly, he will probably assume the artist to be incapable of learning to programme, or at least unwilling to do so. Less surprisingly, he will probably hold the notion that art is principally involved with the production of ‘exciting’ images, and that he will best serve the artist’s needs if he can enable him to produce a large number of widely differing images, all ‘exciting’.

How would it be to try to write poetry by employing a specialist in rhyme-forms? Each time you get to the end of a line you call him up to ask what word he thinks would best convey what you have in mind. The process sounds rather more promising than trying to produce art by getting a specialist to write computer programmes on your behalf. If we are to get past ‘computer-art’, as I am sure we shall, to art made with the help of computers, it will need to be on the basis of a massive change of mental-set on the part of the artist.⁵

Suppose, now, that I have a computer whose abilities are like those I have described. Suppose also that it is connected to a teletype and to a drawing machine (Fig. 5a, b). Assume that the computer has already been loaded with the programme by means of which it will be able to interpret my own instructions. (My instructions here will not be phrased in any existing ‘higher-level’ language but in a fictitious one designed to make clear what is being done. In fact I will describe programmes diagrammatically, by means of what are known as ‘flow-charts’, rather than in the line-by-line form required by every language.) Let’s see if the machine works:

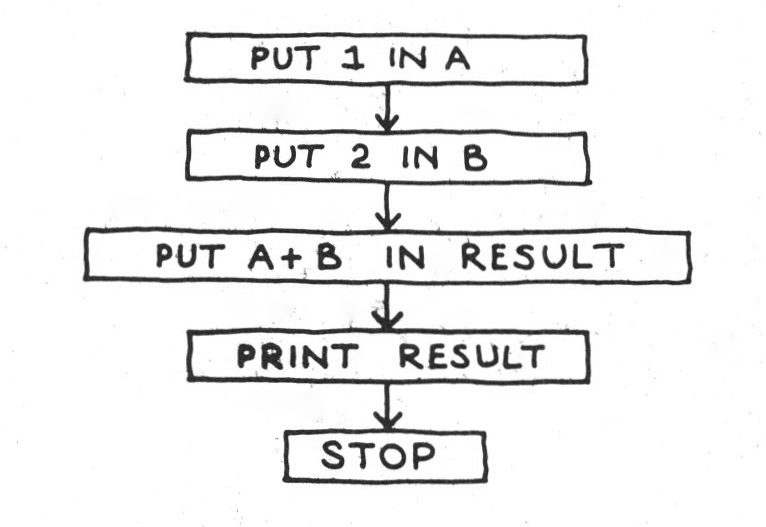
now that this programme has been loaded, I type ‘RUN’ on the teletype, and the machine responds .. . 3. The programme has taken around I /50,000 of a second to run — the teletype, being mechanical, takes much longer to operate, of course — and we know that the machine can figure out that 1+2=3. Let’s try something a bit more complicated:

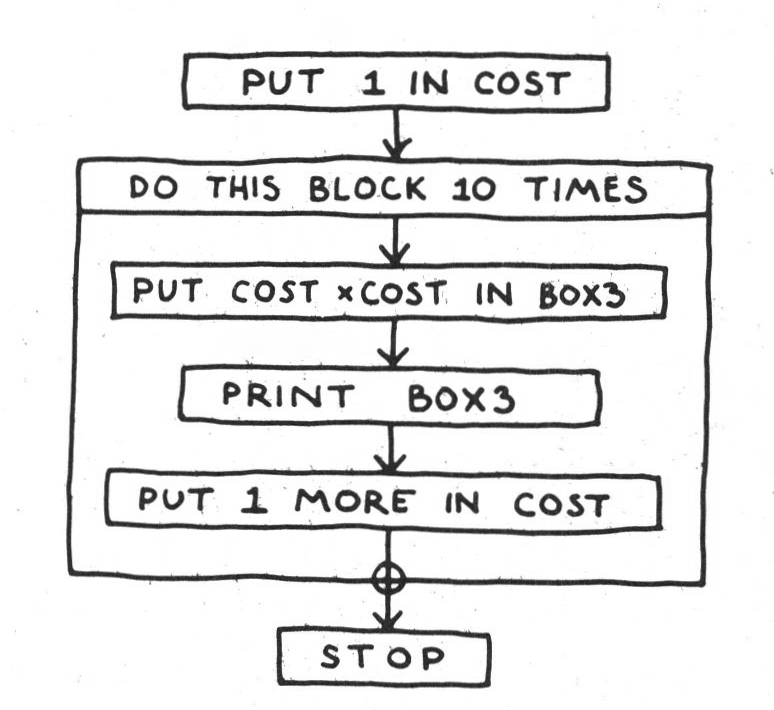
this time, when I have loaded the programme and type ‘RUN’, the machine will get the I it has just put in the cell labelled COST, square it, store the result in BOX3, and then print out that result. But then, instead of stopping, it will add i to the i already in COST, and go through the whole cycle again, printing out 4 this time, and then 9, 16, 25, and so on until it has completed the ten re-iterations called for.

This is pretty simplistic, of course, involving a lot of unnecessary PUTting and GETting into and out of memory. If the machine’s language were a little more sophisticated, we could have written the programme:

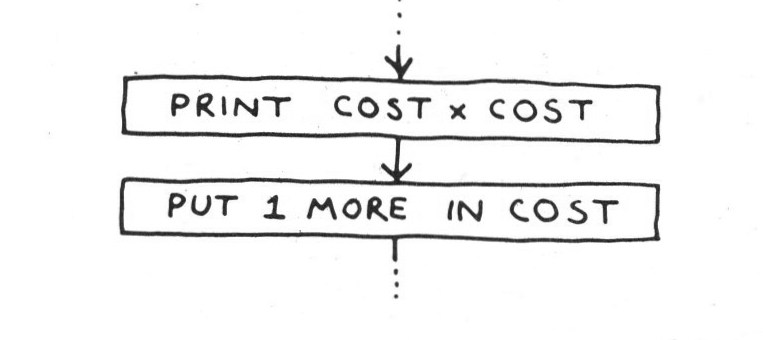
with exactly the same result. Note how powerful a device it is that instead of saying first ‘print the square of then ‘print the square of 2’, then ‘print the square of 3’, we need only say, ‘print the square of whatever is in the cell labelled COST’, repeating the same instruction every time. All that changes is the contents of the cell COST. This notion of referring to a number by the name on its cell is fundamental to programming, and in fact it is something we do all the time ourselves. Saying that a carpet is ten feet long and seven feet wide is essentially like saying:

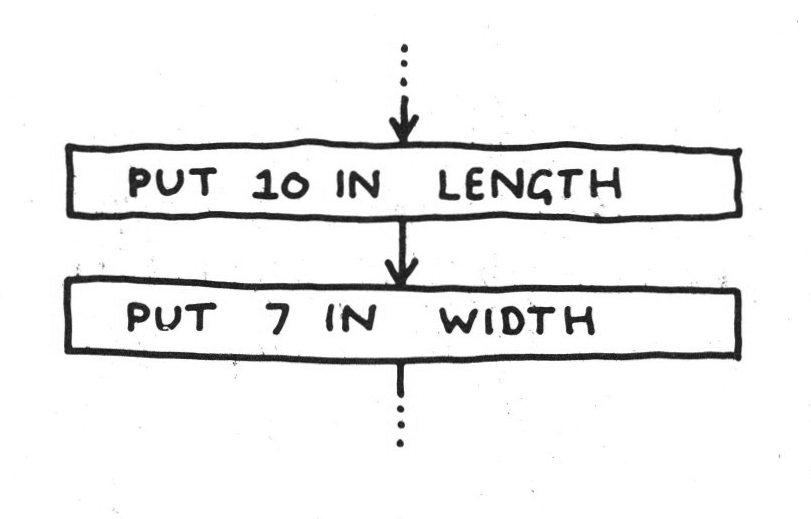
and we could obviously build this into a programme for finding the area of the carpet by adding

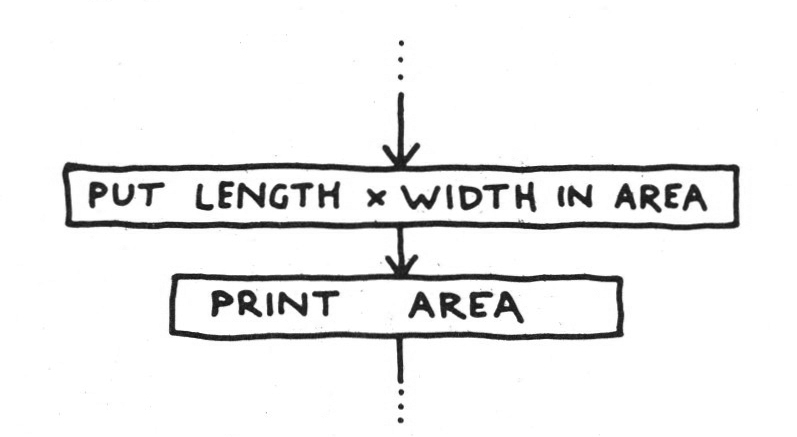
the important thing here is the level of generality, since the programme will now work for whatever values we put in the cells labelled LENGTH and WIDTH.

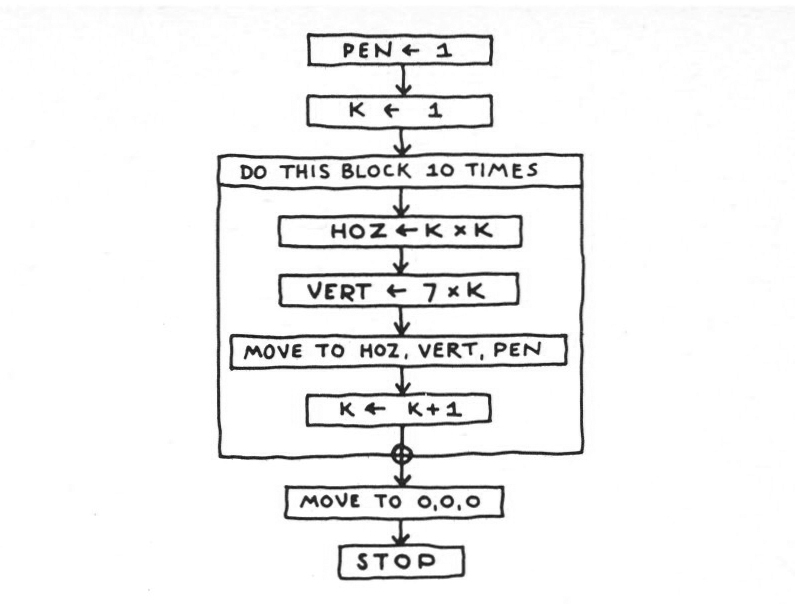
We should be able to get the drawing machine to draw something now. You will probably remember the idea that you can describe the position of any point on a sheet of paper by two distances, or coordinates: how far the point is horizontally from the left hand edge and how far it is vertically from the bottom. Suppose we were to reserve two cells labelled HOZ and VERT for storing the two coordinates for any point to which we wanted the pen to go. If the pen is sitting in the bottom left hand corner, and our programme says:

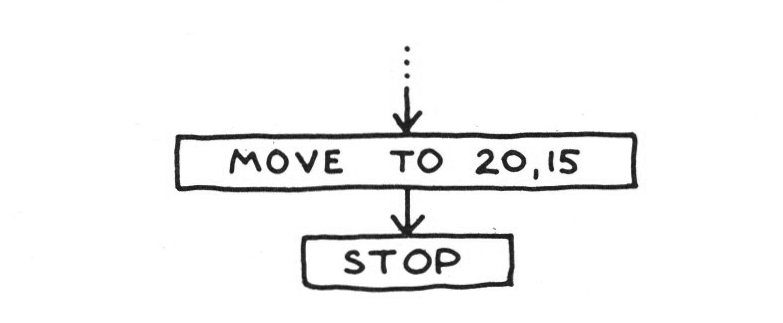
the computer will recognize from the command MOVE that it must send its instructions to the drawing machine, not to the teletype, and will thus send out the commands required to make the pen move to the centre of the bed. The only problem with this programme is that it didn’t specify whether the pen was to be down or up. The programme should probably have read:

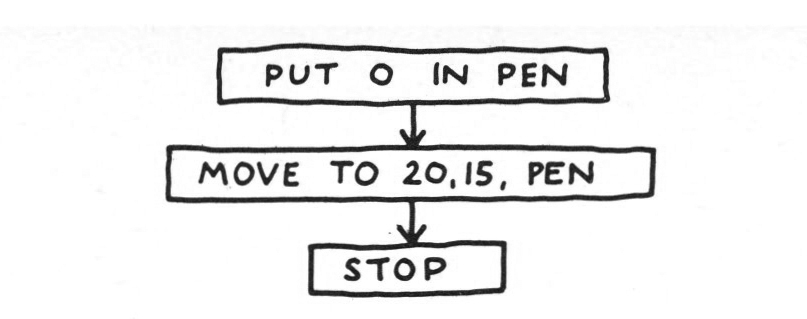
where the cell PEN will hold r as a code for ‘pen down’ and o as a code for ‘pen up’. We might also have generalized a step further, and said: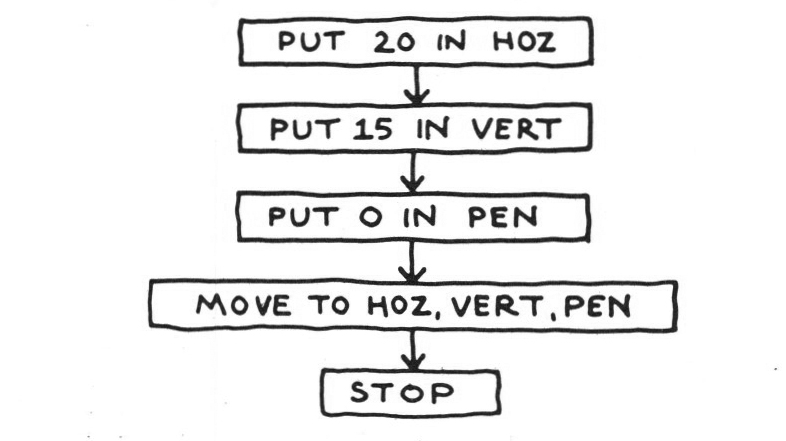

because now we might want to write the sort of reiterative programme we looked at earlier, to draw a whole series of points. In writing such a programme we will now use a shorter notation for PUT, so that instead of writing PUT 5 in HOZ, we would write HOZ<-5.

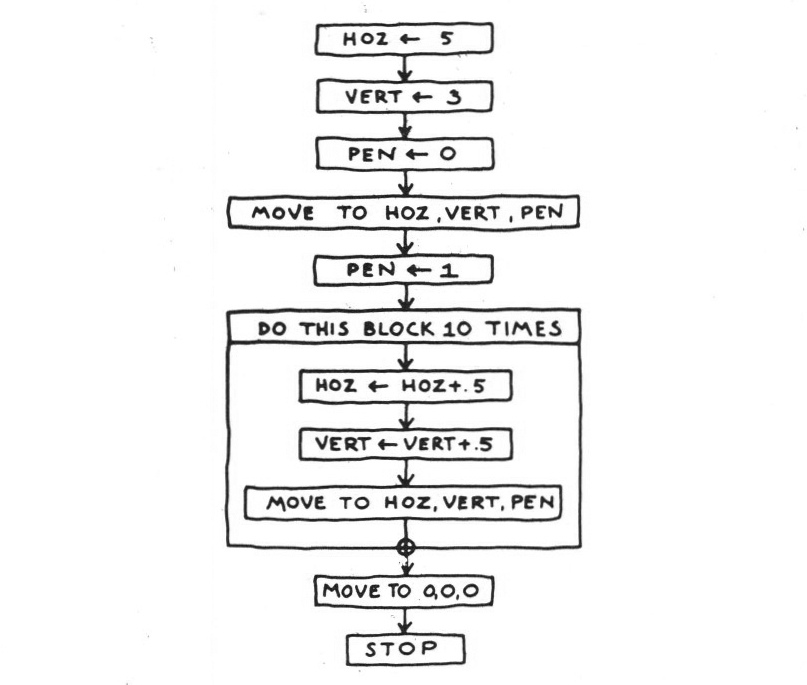
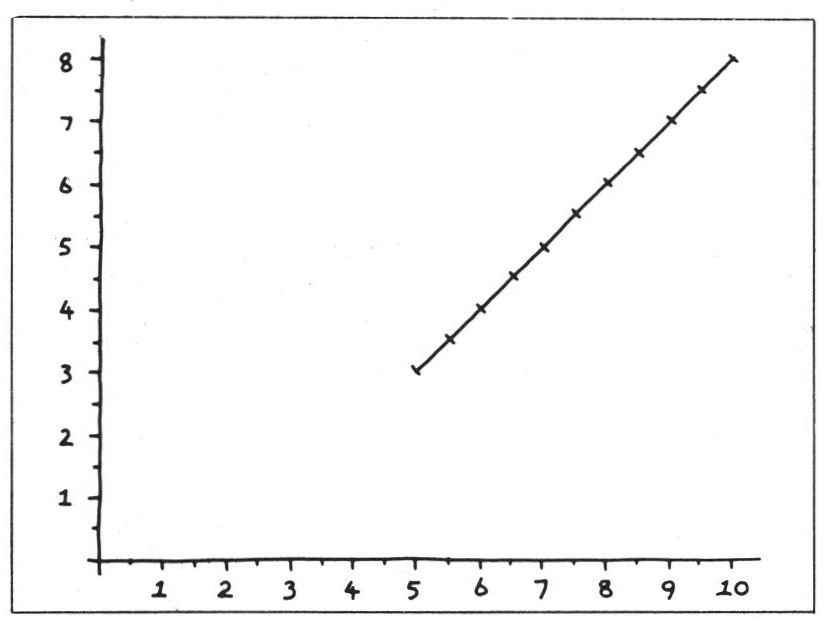
Figure 6.

Not a very exciting drawing, but it does illustrate a lot of principles. You might be surprised by the statement

HOZ<-HOZ+.5

but of course this isn‘t algebra, and it isn’t an equation. It means, simply, ‘take what was in the cell labelled HOZ, add .5 to it and put it back in the same cell’. The pen has drawn a series of ten short line segments which in this case make up a straight line: and has then lifted and gone back to the bottom left hand corner. The same general form will draw lines which are not straight, if we can simply think of a way of generating the appropriate pairs of coordinates. For example:

will produce this curve.

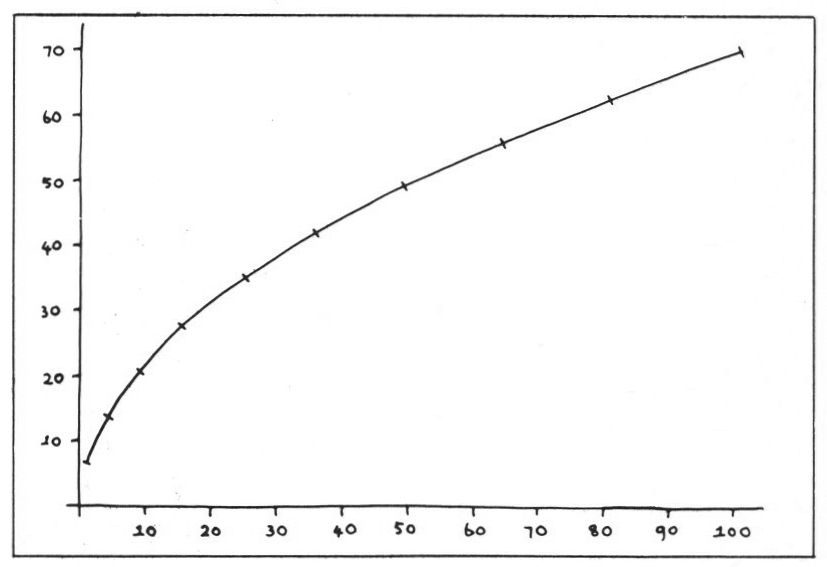
Figure 7.

The thing is that any pair of statements which relate the horizontal coordinate to the vertical in a coherent way will produce some sort of curve, and it’s quite easy at this point to start popping in all kinds of trigonometrical functions and stand back to see what happens. This one was written by a passing computer-science student — I hesitate to say ‘invented’, since it is almost entirely a matter of chance whether it will produce anything pretty, which I think it does.

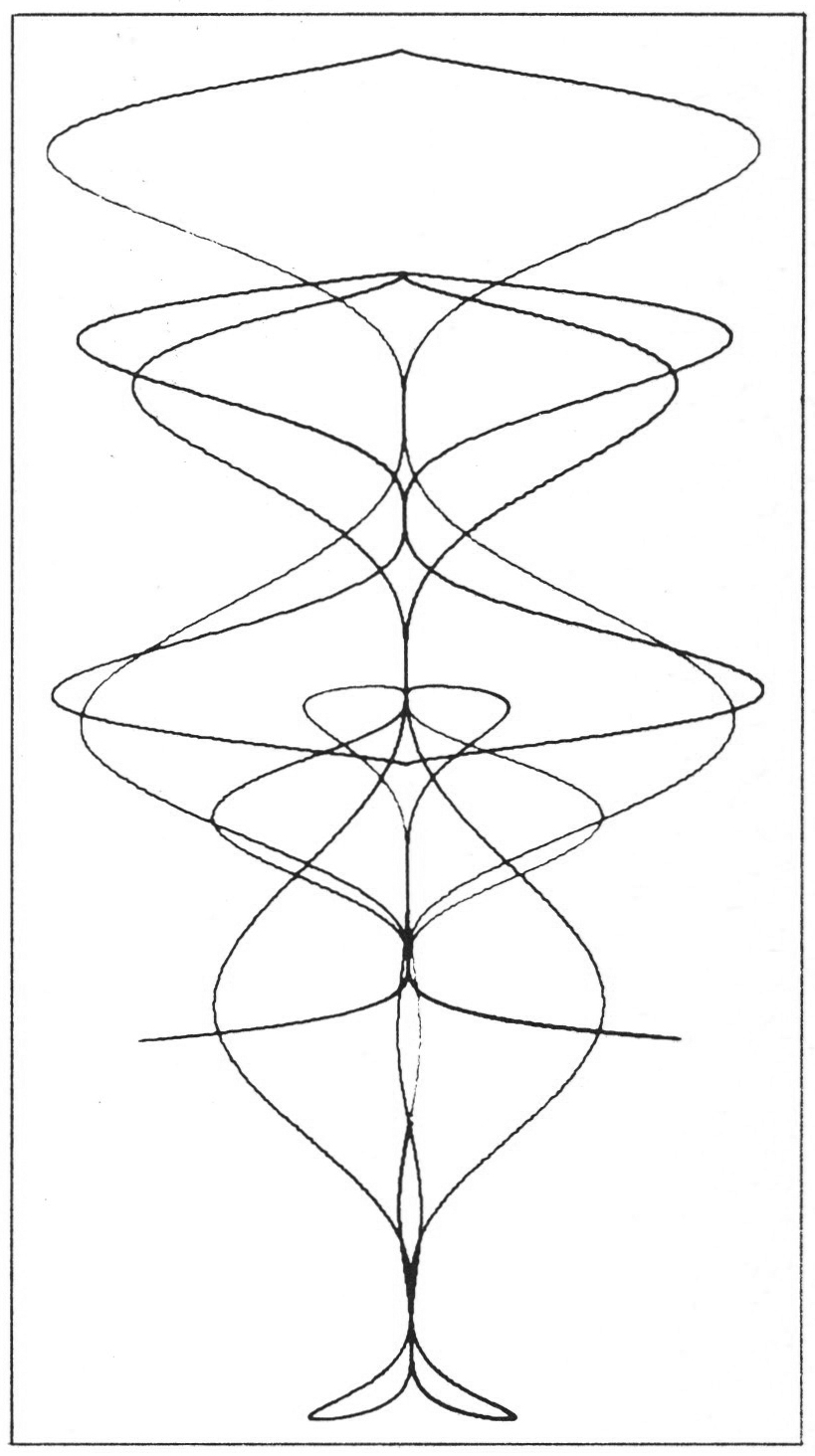
Figure 8.

No doubt the introduction of this sort of technique for drawing curves into ‘computer art’ owes much to the mathematics-oriented programmer, who would tend to view a curve essentially as the graph of a mathematical function. But not all curves can be handled in this somewhat simplistic way, and artists wishing to handle more complex curves have been obliged mostly to use an entirely different approach, if anything even more simplistic. Since it is possible to describe any point by its HOZ-VERT pair, it follows that any drawing can be approximated by a set of points, each of which can be treated in the same way, so that the whole drawing can be described in purely numerical terms. Imagine then that you have already done a drawing, that you have reduced it to a string of points, and that you have typed the HOZ and VERT values of each point together with its PEN code, on a series of punched cards (or, of course, any other storage medium for which the computer has the appropriate peripheral). A programme like this

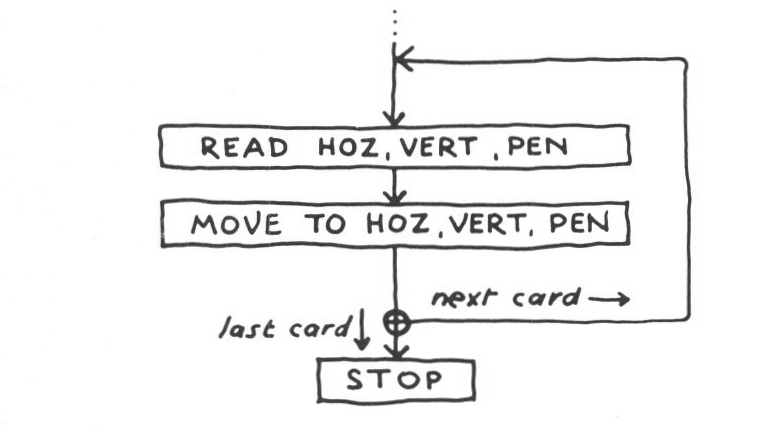
would then simply read the first card to find the first point in the drawing (PEN would presumably be o until it gets here), move the pen to that point, read the next card for the next point, and so on until it has done all the points. The machine has duplicated your drawing from your numerical description.

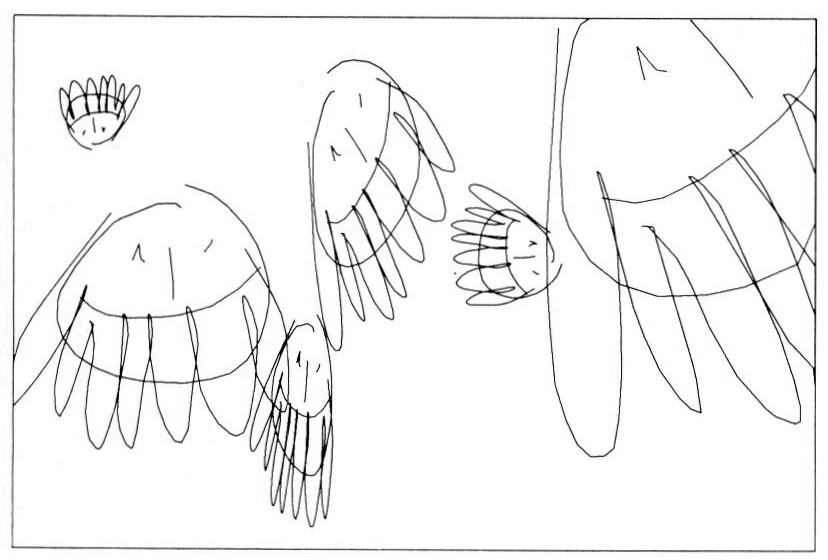
Figure 9.

It may not be clear why anyone would want to use such elaborate means to reproduce a drawing he has already made. The answer is that quite a lot of things can be done to the drawing by suitable programmes. Not only can it be reduced, enlarged, shifted, rotated, squashed up, pulled out (Fig. 9): it can also be transformed as if it were drawn on a sheet of rubber which was then stretched in various irregular ways. None of these operations, or transformations as they are called, is difficult to programme, and since they can be applied to any set of points whether generated from mathematical equations or read in from cards, they have tended to become the stock-in-trade of ‘computer art’. Indeed, it would be difficult to see how any computer animation involving drawn images could proceed without such transformations.

For our purposes, however, the question to be asked is whether the notion of a picture processor, operating upon some previously generated image, corresponds in any useful way to what we know of human art-making behaviour. I think the answer has to be that it does not. To achieve that correspondance, the machine would need to generate the image, not merely to process it.

Intuitively, it seems obvious that the human process involves characteristics which are quite absent from these procedures, and in particular I think we associate with it an elaborate feedback system between the work and the artist; and dependent upon this system are equally elaborate decision-making procedures for determining subsequent ‘moves’ in the work. Our enquiry might reasonably proceed by examining whether the machine is capable of simulating these characteristics.

Before going on, I must explain that the computer possesses one significant ability which was implied by the earlier examples but never explicitly stated. It is able to compare two things, and on the basis of whether some particular relationship holds between them or not, to proceed to one of two different parts of the programme. In practice this primitive decision-making device can be built into logical structures of great complexity; with the alternative paths involving large blocks of programme, each containing many such conditional statements, or ‘branches’.

It would be quite difficult to demonstrate a complex example here in any detail. The drawing on the cover of this issue of Studio International was generated by a programme of about 500 statements, of which over 50 were concatenated from these simple conditionals, equivalent to about 85 branches. We might look at one part of that programme, however, about 50 statements in all, which generates the individual ‘freehand’ lines in the drawing. Obviously the flow-chart is a much-simplified representation.

The argument behind the sub-programme runs like this: in any ‘sub-phase’ of a line’s growth it will be swinging to the left or to the right of its main direction (‘straight on’ if given by swing= o). This swing may be constant, accelerating or decelerating, and both the rate of swing and the rate of change of swing may be either slow or rapid. Overall, the line must not swing beyond a certain pre-set angle from its main direction. A single full phase will consist of two sub-phases normally swinging in opposite directions. Both of these, and the phase itself, may vary in length, and normally the starting direction for each full phase does not depend on that of the previous one.

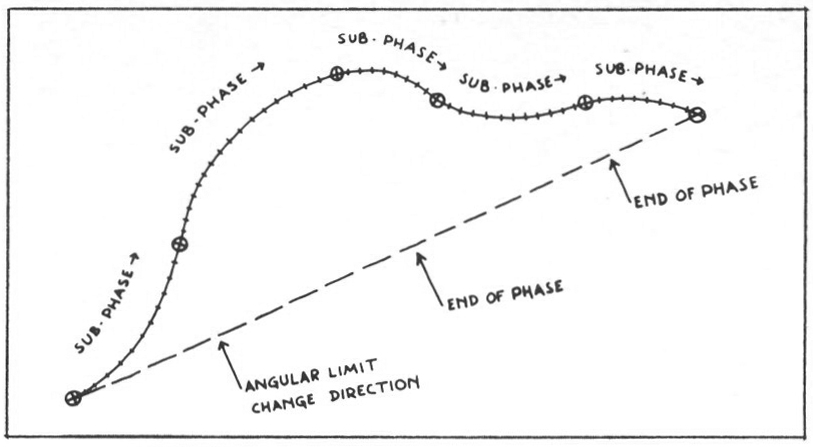
Figure 10.

If the line swings beyond its angular limit, however, all the factors controlling the current phase are immediately reset and a new full phase is initiated, starting off in the opposite direction. It should be noted also that the line has some definite destination and corrects continuously in order to get to it. The programme would look something like this:

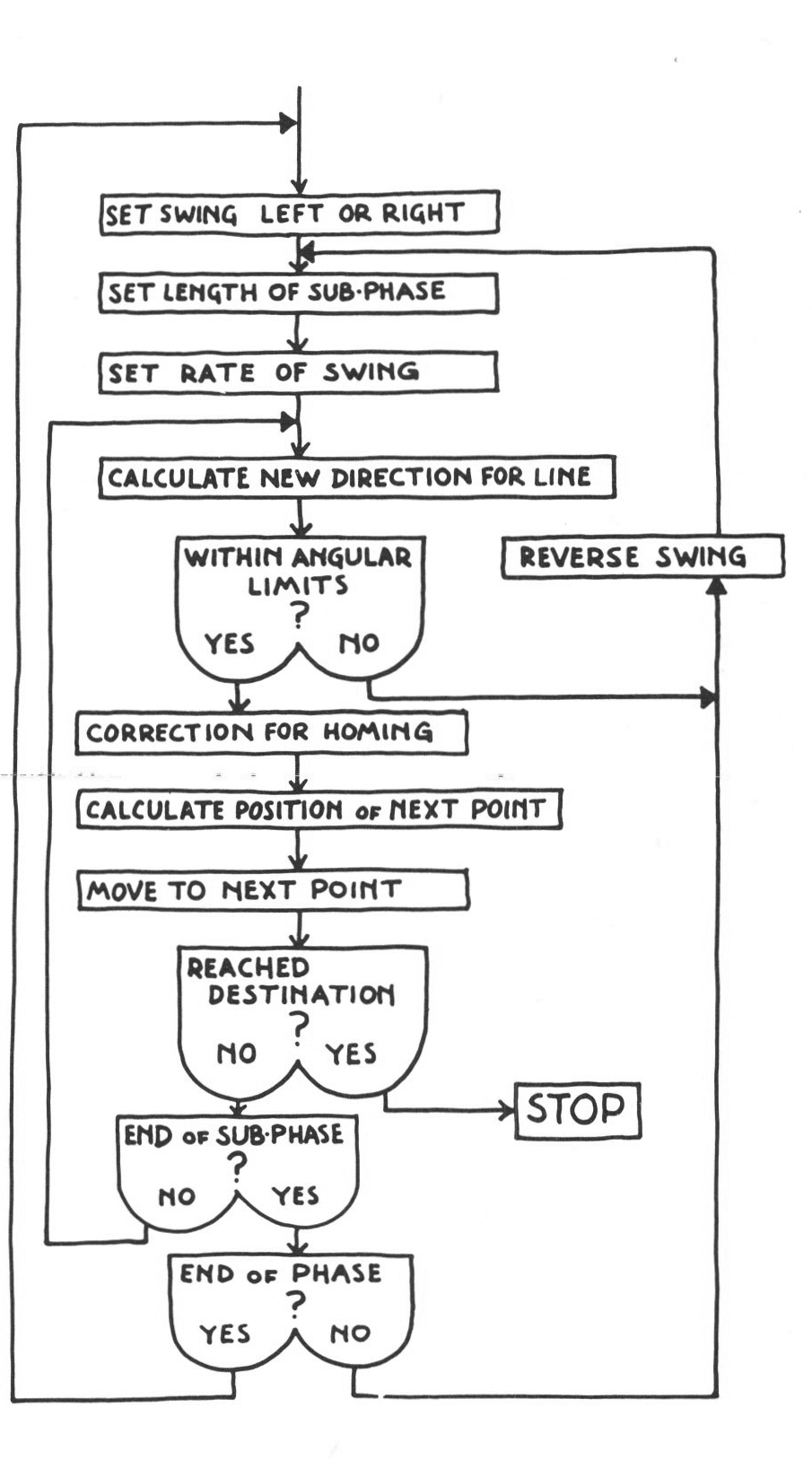
this structure does evidently possess a feed back system not unlike the kind we employ in driving a car. There is an overall plan — to reach a destination — which breaks down into a succession of sub-plans, which are in turn responsible for generating a series of single movements. But if an ‘emergency’ is signalled, the current sub-plan is abandoned, and a new one set up.

The quality of the line is directly related to the way in which the factors for each new sub-phase are reset : if the length of each sub-phase varies enormously, or if the rate of change of swing varies greatly from one to the next, the line will tend to be quite erratic. If the angular limits are set quite small — by the over-all plan — then the line as a whole will be more ‘controlled’. How does the programme ‘decide’ on new factors for each new sub-phase? The ranges permissible for each factor are precisely determined in relation to what the range was last time, indicating another level of feedback. Within that range, the machine makes a random choice.

There seems to be so much popular misunderstanding about the nature of randomness that a word might be said on the subject before going further. Contrary to popular belief, there is no way of asking the machine to draw ‘at random’, and if you try to specify what you mean by drawing ‘at random’ you will quickly see that what you have in mind is a highly organized and consistent behavioural pattern, in which some decisions are unimportant provided they are within a specified range of possibilities. This is characteristic of directed human behaviour: if you plan to rent a car, you will probably be concerned that it should be safe, that its size and power will be appropriate to your needs. You probably won’t care too much what colour it is, and in being prepared to take whatever comes you are making a ‘random choice’ of colour: although you probably know it isn’t likely to be iridescent pink, matte black, or chromium plated. The same might be said – though with much narrower limits – of the painter who tells his assistant to ‘paint it red’; or indeed the painter who uses dirty brushes to mix his paint. They are all examples of making a random choice within specified (or assumed) limits. In fact the computer generates random numbers between zero and one, which must then be scaled up to limits specified by the user’s programme.

You might consider that, in human terms, these limits will be narrow where precise definition is required, wide where it is not. For the computer, the existence of limiting ranges rather than specified values will result in the possibility of an infinite number of family-related images being produced rather than a single image made over and over again. There might be some difficulty in demonstrating the case to be otherwise for the artist.

While it would seem obvious that any complex purposeful behaviour must make use of feedback systems, there is no suggestion that such systems alone can account adequately for the behaviour. Moreover the ability to satisfy some given purpose, as the ‘freehand’ line generator does in homing on its destination, accounts for only slightly more. The formulation of the purpose is something else : and we would expect to find in human art-making behaviour not only a whole spectrum of purpose-fulfilling activities, but also a spectrum of purpose-formulating activities. If I am to pursue my enquiry, I must now try to demonstrate the possibility of such a structure occurring in machine behaviour, although the strategies employed within the structure may or may not correspond to the strategies the artist might employ. Certainly no such claim will be made for the programme I am about to describe.

This programme is one of a series in which the principal strategy is devised in relation to an ‘environment’ which the programme sets up for itself. An example would be one in which the programme first designs, and then runs, a maze: the resultant drawing being simply the path generated by the machine in performing the second part. In the present programme, the environment is a rectangular grid of small cells, into which are distributed sets of digits (Fig ix.) The strategy adopted in the second part involves starting at a from there seeking to draw a line to a ‘2’, then to a ‘3’ and so on. The digits are considered as a continuous set, ‘to’ being followed by ‘I’, so that but for three things the programme would continue indefinitely. The first is that no digit may be used as a destination more than once, and since a digit is also cancelled if a line goes through its cell, the number of destinations steadily reduces, and the programme terminates. The second is that a destination will not be selected if getting to it involves crossing an existing line, so that finding a destination becomes more difficult as the drawing proceeds. And the third is that there are certain ‘preferences’ operating in choosing between those destinations recognized by the machine as viable. As a consequence of these constraints, the machine will eventually find itself unable to continue to the next digit, and it will then back up to the previous digit on its part and attempt to go on again from there. The drawing will be complete when the back-up procedure has taken it all the way back to the original ‘I’.

Now it is possible, by manipulating the factors controlling the machine’s ‘preferences’ — I will say more about those in a moment — and by appropriately setting various other factors, to produce a very wide range of characteristics in the drawings produced.

Figures 11 and 12.

For example, the number of cells in the grid and the number and type of distributions of the digits are both critical factors in determining the complexity of the drawing. Under studio conditions I have varied these factors myself, but for a recent exhibition I wrote an executive programme which took over that task: and under its control the machine produced almost three hundred drawings during the four weeks it was in the museum. These varied from a few squiggly lines to quite complex drawings, from a single large image to anything up to twelve small ones on a page; and they required no human participation beyond changing the paper and refilling and changing pans.⁶ (Fig. 13.)

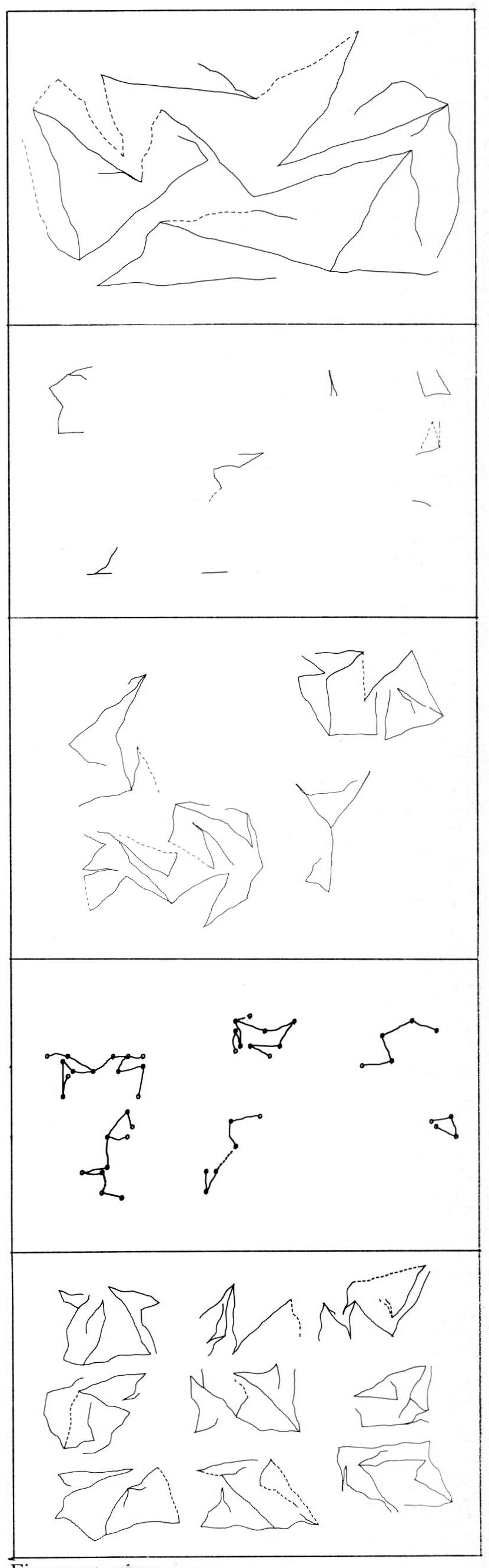
Figures 13 a, b, c, d, e.

What I have described as being controlled by the executive is, in a very general sense, the purpose-formulating mechanism for the ‘freehand’ line generator, the structure that determines where the lines are to be drawn. You might say that I am the purpose-formulating mechanism for the programme as a whole, but the executive programme makes my own part in the process rather more remote, if no less significant. In fact, I doubt whether the main programme will be changed much at this point, since what is at stake for me is not what it does, but what determines what it does. I am referring to the ‘preferences’ mentioned earlier.

As it reaches each destination, the machine has to choose between anything up to twenty-five next destinations, depending upon the state of the drawing. In the present state of the programme, its preference is for destinations within certain distance limits, but it is easy to see how it might ‘prefer’ long lines to short ones, a destination near the centre of the picture, or in highly active parts of the picture: or it might ‘prefer’ the one involving minimum change of direction; or the reverse of any of these. Obviously the character of the resultant drawings would vary enormously as the machine exercised one ‘preference’ rather than another, but in fact I am suggesting something more complex than simply switching ‘preferences’. Suppose, rather, that the machine exercises its whole range of ‘preferences’ by scoring each possible destination for its ability to satisfy each preference, and taking the destination with the highest total score as its choice. It might then choose the destination which was relatively far away, didn’t involve too much deviation from the current direction, and was in an area of high activity quite close to the centre of the drawing. I think this would be a much closer simulation of the way in which human preference-structures are exercised.

Let us go one step further, and suppose the machine to be capable of weighting its scores for its different ‘preferences’, and of modifying these weightings itself. This possibility is by no means speculative: readers familiar with the development of the field of Artificial Intelligence will recognize its similarity to Samuel’s now classic programme for a checkers-playing machine (1959). They will recall also that the programme enabled the machine to learn to play, by having it play against itself, one part always adopting the best strategy found to date, the other varying the weightings of the ‘preferences’ which determined that strategy until it found a better one, and so on. In a short time it was able to win consistently against any human player.

We might recognize a significant difference between applying a learning programme of this sort to successful game playing and doing so to successful art-making. Of course the difficulty is ours, not the machine’s: since we ourselves would be in some doubt as to the nature of the criteria towards the satisfaction of which the machine might aim. Art is not a deterministic game like checkers, to be won or lost by the ‘player’; and though we acknowledge, empirically, that some artists are ‘better’ than others, that some artists do improve, the problem of formulating general criteria for improvement may be no different in relation to the machine than it is for the teacher in relation to the art student. It is probably reasonable to assume that there do exist criteria at levels even more remote from the work than any I mentioned: in which case we should be able to formulate them and the machine should be able to satisfy them. But there remains the suspicion that satisfactory performance in art is not to be measured solely by the satisfaction of explicit criteria, and would still not be so no matter how far back one pushed.

As to those explicit criteria: there would seem little reason to deny that the machine behaves purposefully at every level described. Yet no level defines its own purpose. The learning level would — but for the difficulties mentioned above — advise the preference-structure as to the best way of defining the manner in which the executive commands the main programme to select the points between which the ‘freehand’ line generator is to draw lines. One might say even that the purpose of each level is to formulate the purpose for the next level. It is true, of course, that the machine’s organization is that way because it has been set up that way, but in considering the nature of explicit criteria in human art-making behaviour we might reasonably adopt the machine’s organization as a model, and say that these criteria relate to the formulation of new levels of purpose in satisfaction of prior purposes. This can be maintained without any suggestion that the machine can move higher and higher up the ladder until it is finally in possession of the artist’s Purpose. On the contrary, it seems to me that pushing back along the chain of command — either for the machine or for oneself — is less like climbing a ladder than it is like trying to find the largest number between zero and one: there is always another midway between the present position and the ‘destination’.

It should be evident, then, that I do not consider ‘serving the artist’s Purpose’ to be equivalent to ‘talking over the artist’s Purpose’, or identify the machine with the artist. I identify the artist with the whole Purpose-structure, the machine with the processes which are defined by the structure and in turn help to redefine it. Since under other circumstances these processes too would be played out by the artist, I am also identifying playing-out with the computer with playing-out without the computer. For the machine to serve his Purpose the artist will need to use it as he uses himself. There is no reason to anticipate that the use will be more or less trivial than the use he makes of himself, but every reason to suppose that the structure will change in ways which are presently undefinable.

The step by step account of the computer’s functions and its programmes was intended, of course, to try to demonstrate that the machine can be used in this way. The original question — whether the machine can serve the artist’s Purpose - is more redundant than unanswerable, and is in any case not to be confused with asking whether artists might see a need to use it. It is characteristic of our culture both that we search out things to satisfy current needs, and also that we restate our needs in terms of the new things we have found. Nor is it necessarily immediately clear what wide cultural needs those things might eventually serve. The notion of universal literacy did not follow immediately upon the development of moveable type, but it did follow that development, not demand it. Up to this point the computer has existed for the artist only as a somewhat frightening, but essentially trivial toy. When it becomes clear to him that the computer is, in fact, an abstract machine of great power, a general purpose tool capable of delimiting his mind as other machines delimit him
physically, then its use will be inevitable.

(Photographs for this article by Becky Cohen.)

References

1. I wish I had more space here to develop and justify what may seem to be extravagant views. Readers wishing to pursue the issue for themselves will find these views to be almost timid compared to the current rate of growth and technological development within the industry. There is extravagance indeed! Of an estimated 80,000 computers now operating in the US alone, 13,000 were installed in 1972 by a single manufacturer. Spending on small computers is projected by a leading magazine to rise to $600,000,000 a year in the US by 1975.

2. But not necessarily for other times and other cultures.

3. Recursion is a powerful mathematical concept which is difficult to describe in non-mathematical terms: indeed, the above examples are as good as any I have been able to find. If you think of a mathematical function as being a structure which operates upon something provided to it, then a recursive function is one which provides itself with the ‘something’ by its previous operation. Since the ‘something’ will be different for each operation, this is not to be confused with circular structures: e.g. art is something produced by an artist, an artist is someone who makes art. Also, the idea of the boy holding the bag of popcorn on which there is a picture of the boy holding the bag of popcorn on which ... actually represents a hierarchical structure rather than a recursive one.

4. I am not making this up. See ‘Idols of Computer Art’ by Robert E. Meuller, Art In America, May, 1972 : and my own reply in ‘Commentary’ in the following issue.

5. Under grant number A72-I-288 from the National Endowment for the Arts, Washington, DC I am currently investigating the feasibility of setting up a Centre for Advanced Computing in the Arts. One might speculate that, among other things, such a centre might enable artists to use the machine for their own purposes, rather than presenting them with a cookery book of possibilities.

6. ‘Machine Generated Images’, La Jolla Museum, California. October-November 1972. The drawings reproduced here are taken from the show. The machine was able to make drawings in several colours, but the museum staff had some difficulty in following its instructions for mounting the appropriate pens. In the event, it was limited to asking for the correct size pen to be mounted.